About

I'm an Associate Research Scientist in the Center for Computational Mathematics and the Center for Computational Biology at the Flatiron Institute interested in numerical analysis and scientific computing. I received my Ph.D. in applied mathematics from Harvard University, where I was advised by professors Alex Townsend and Chris Rycroft. My research focuses on spectral methods, fast methods for PDEs, computational fluid & solid mechanics, and multigrid methods. In the past, I have worked at Walt Disney Animation Studios, Lawrence Berkeley National Laboratory, Wolfram Research, and Apple.

Research

Surface PDEs

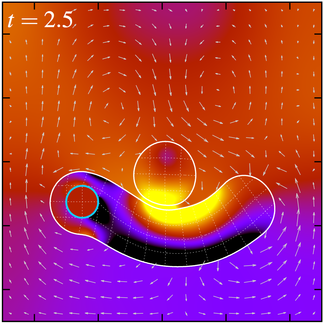
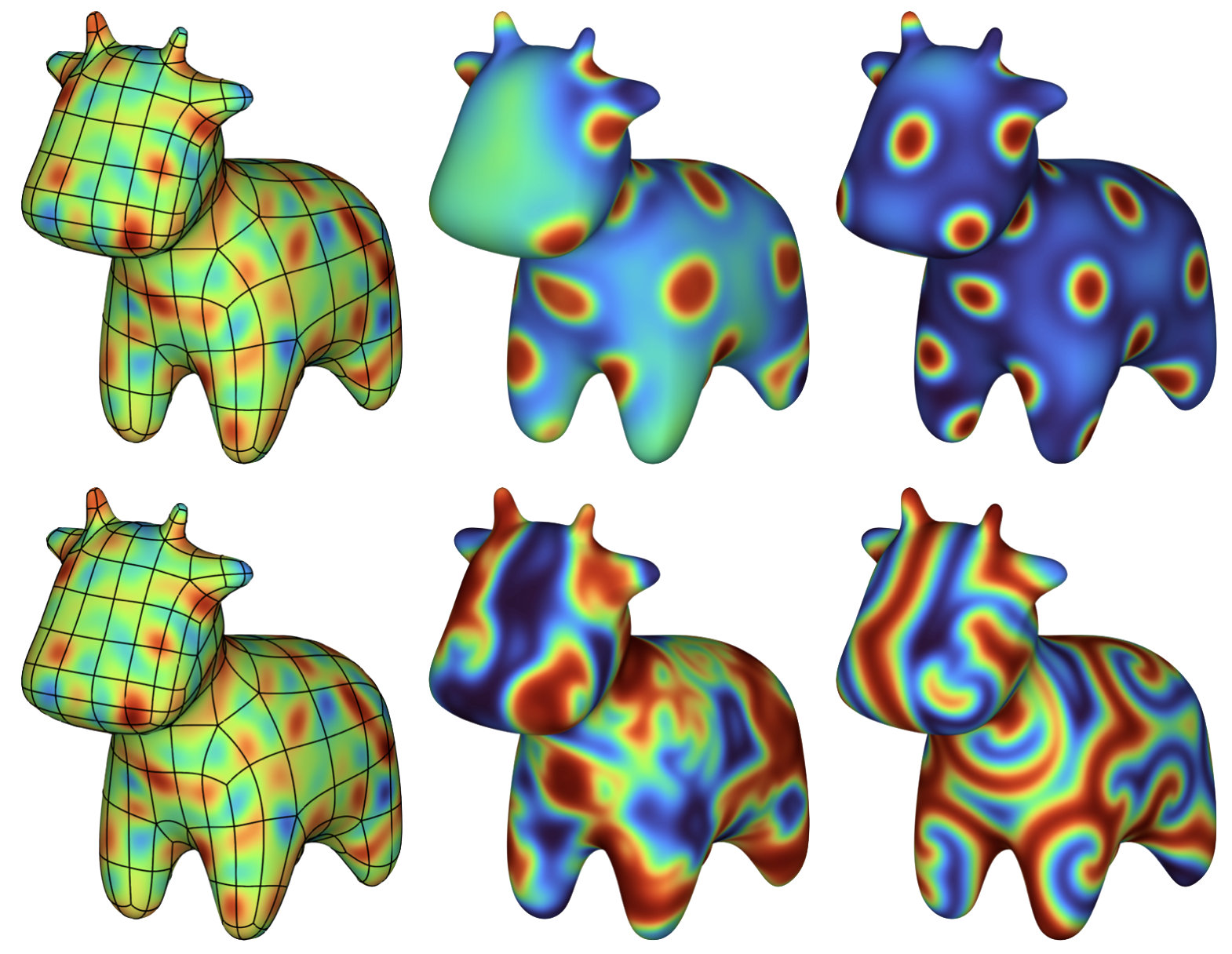
I have developed a high-order accurate fast direct solver for variable-coefficient partial differential equations on surfaces, based on spectral collocation and the hierarchical Poincare–Steklov scheme. The method may be used to accelerate implicit time-stepping schemes as repeated solves require only \(\mathcal{O}(N \log N)\) work on a mesh with \(N\) elements, after an \(\mathcal{O}(N^{3/2})\) precomputation. I have applied it to a range of scalar- and vector-valued problems on both smooth surfaces and surfaces with sharp corners and edges, including the static Laplace–Beltrami problem, the Hodge decomposition of a tangential vector field, and some time-dependent reaction–diffusion systems.

Spectral methods

In collaboration with Alex Townsend and Nick Hale, I have developed the ultraspherical spectral element method, a sparse spectral element method suitable for \(hp\)-adaptivity with very high \(p\). The method is based on the hierarchical Poincare–Steklov scheme and has a computational complexity of \(\mathcal{O}(p^4/h^3)\).

In collaboration with Alex Townsend, I have developed spectrally accurate Poisson solvers for the square, cylinder, solid sphere, and cube that have optimal complexity (up to polylogarithmic factors). The solver is based on the ultraspherical polynomials and the alternating direction implicit (ADI) method.

Computational fluid & solid mechanics

In collaboration with Chris Rycroft and Robert Saye, I am developing a high-order Eulerian method for fluid–solid interaction based on the discontinuous Galerkin and level set methods.

Multigrid methods

In collaboration with Robert Saye and Chris Rycroft, I have developed efficient multigrid schemes for local discontinuous Galerkin methods that are robust with respect to mesh size and polynomial order. The method is based on coarsening the divergence and gradient operators separately.

In collaboration with Rasmus Tamstorf, Steve McCormick, and Toby Jones, I implemented an algebraic multigrid method for cloth simulation based on adaptive smoothed aggregation.

Papers

  1. K. J. Burns, D. Fortunato, K. Julien, and G. M. Vasil, Corner cases of the generalized tau method, submitted.   arXiv   PDF
  2. P. Miller, D. Fortunato, M. Novaga, S. Shvartsman, and C. Muratov, Generation and motion of interfaces in a mass-conserving reaction-diffusion system, to appear in SIAM J. Appl. Dyn. Syst.   arXiv   PDF
  3. D. Fortunato, A high-order fast direct solver for surface PDEs, to appear in SIAM J. Sci. Comput.   arXiv   PDF
  4. P. W. Miller, D. Fortunato, C. Muratov, L. Greengard, and S. Shvartsman, Forced and spontaneous symmetry breaking in cell polarization, Nat. Comput. Sci., 2 (2022), pp. 504–511.   DOI   PDF   News (Nature)   News (AMS)
  5. D. Fortunato, N. Hale, and A. Townsend, The ultraspherical spectral element method, J. Comput. Phys., 436 (2021), pp. 110087.   arXiv   DOI   PDF
  6. D. Fortunato and A. Townsend, Fast Poisson solvers for spectral methods, IMA J. Numer. Anal., 40 (2020), pp. 1994–2018.   arXiv   DOI   PDF
  7. D. Fortunato, C. Rycroft, and R. Saye, Efficient operator-coarsening multigrid schemes for local discontinuous Galerkin methods, SIAM J. Sci. Comput., 41 (2019), pp. A3913–A3937.   arXiv   DOI   PDF
  8. A. Mijailovic, B. Qing, D. Fortunato, and K. Van Vliet, Characterizing viscoelastic mechanical properties of highly compliant polymers and biological tissues using impact indentation, Acta Biomaterialia, 71 (2018), pp. 388–397.   DOI   PDF
 Ph.D. Thesis:  
D. Fortunato, Fast Solvers for Elliptic Partial Differential Equations Based on Spectral and High-Order Methods, Harvard University (2020).   Harvard   PDF

Talks

  • A fast direct solver for surface PDEs (2022)   PDF
  • A fully adaptive Poisson solver for smooth two-dimensional domains (2021)   PDF
  • Modern spectral methods (2021)   PDF
  • The ultraspherical spectral element method (2019)   PDF
  • Fast Poisson solvers for spectral methods (2019) [Awarded a second place Leslie Fox Prize]   PDF
  • Efficient operator-coarsening multigrid schemes for local discontinuous Galerkin methods
    (2018)   PDF
  • Fast and accurate element methods (2017)   PDF
  • A fast spectrally accurate Poisson solver on rectangular domains (2017)   PDF

Software

I contribute to a number of open source software projects:

  • surface-hps — A MATLAB package for numerically computing with functions on surfaces.
  • ultraSEM — An implementation of the ultraspherical spectral element method.
  • treefun — A MATLAB package for numerically computing with piecewise polynomials on adaptive trees.
  • surface-diffusion — Spectral methods for reaction-diffusion systems on axisymmetric surfaces.
  • spherical-harmonic-interfaces — A unified MATLAB interface to spherical harmonic transform libraries.
  • multigrid-ldg — Efficient multigrid methods for local discontinuous Galerkin discretizations in C++.
  • fast-poisson-solvers — A repository of fast spectrally accurate Poisson solvers on a variety of domains.
  • Chebfun — A MATLAB package for computing with functions to about 15-digit accuracy. Among other features, I implemented the fast Poisson solver used in chebfun2.poisson.

Projects

Notes